Самая сложная задача по математике, Самые сложные нерешенные математические задачи

Grigoriy Perelman Архивировано 22 марта года. Такси: беседуем обо всём часть 38 Одна лошадь из 18 оказалась как бы «лишней» — это заимствованная лошадь, которую следует вернуть владельцу после раздела имущества. Второй: Ах вот как! Примеры решений задач по высшей математике На этой странице мы собрали простые и сложные примеры из курса высшей математики - от векторов и матриц до дифференциальных уравнений.
Итого в большом ведре остаётся 8 литров. Из меньшего выливаем всю воду обратно в реку и переливаем из девятилитрового в пятилитровое 5 л, после чего в большом ведре останется как раз 3 л воды.
Есть две комнаты с низкими потолками.
В первой висит три лампы накаливания, а в другой установлено три переключателя. Можно сколько угодно раз щёлкать переключатели, но в комнату с лампочками разрешено перейти только один раз. Как узнать, к какому переключателю подсоединена каждая из лампочек? В условии сказано, что комнаты с низкими потолками, а перед нами лампы накаливания — то есть они нагреваются. Нам достаточно включить любую из них на некоторое время, затем выключить её и включить любую другую. После этого переходим в комнату с лампочками:.
А как насчёт такой логико-математической задачи? Предположим, у нас есть две верёвки и бесконечное множество спичек.
Каждая из этих верёвок сгорает за один час. Но вот беда — горят они неравномерно, поэтому невозможно узнать наверняка, за какое время сгорит какая-то часть веревки.
Можно ли отмерить этими двумя верёвками 45 минут, и если да, то как это сделать?
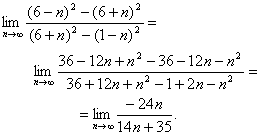
Отмерить можно. Пусть верёвки и горят неравномерно, но сгорают они точно за 1 час. В этом случае можно:. Есть двадцать баночек с таблетками. Почти во всех таблетки весят по 1 г, и только в одной — по 1,1 г.
У нас есть точные кухонные весы, с помощью которых нужно определить баночку, каждая таблетка которой весит 1,1 г. Как это сделать, если можно взвесить только 1 раз?
Представим, что у нас 2 баночки, в одной из которых таблетки более тяжёлые. Это очень важно для криптографии, но даже самый мощный суперкомпьютер не может исследовать все значения до бесконечности, поэтому необходимо какое-то четкое доказательство для всех натуральных чисел.
Эта проблема была сформулирована Кристианом Гольдбахом в году в письме к Леонгарду Эйлеру, другому мастеру математики.
Сам Кристиан выразил ее более просто: «Каждое нечетное число больше пяти может быть выражено как сумма трех простых». В году перуанский математик Харальд Хельфготт нашел окончательное решение этой задачи для трех простых чисел.
Однако следствие из этого утверждения, предложенного Эйлером, называется «биномиальной проблемой Гольдбаха», и никто до сих пор не смог ее решить. Это одна из самых старых нерешенных математических проблем, известных человечеству. Она относится к нерешенным математическим проблемам, поскольку математики до сих пор не смогли доказать гипотезу чисел-близнецов.
Числа-близнецы - это простые числа, которые отличаются только на два. Например, 11 и 13, а также 5 и 3 или и Как это обычно бывает в математике, когда проблема не решается «с головы», к ней подходят с другой стороны.
Например, в году было доказано, что количество простых чисел с разницей в 70 миллионов бесконечно. А менее чем через месяц эта разница была улучшена на порядок - до 59 , а затем до 4 Хотя теоретически обосновано, что существует бесконечно много пар простых чисел с разностью 12 и 6, были получены доказательства лишь для различий. Дальше будет неравнество вида Его можно Ведь если x меньше N, то и floor x будет меньше. А в противном случае floor целое N не перепрыгнет никак.
Это число, для сокращения выкладок ниже, назовем. Итак, пробегает значения от до , а внутри происходит сумма скольки-то единиц. Их количество мы уже считали выше. Итоговая формула:.
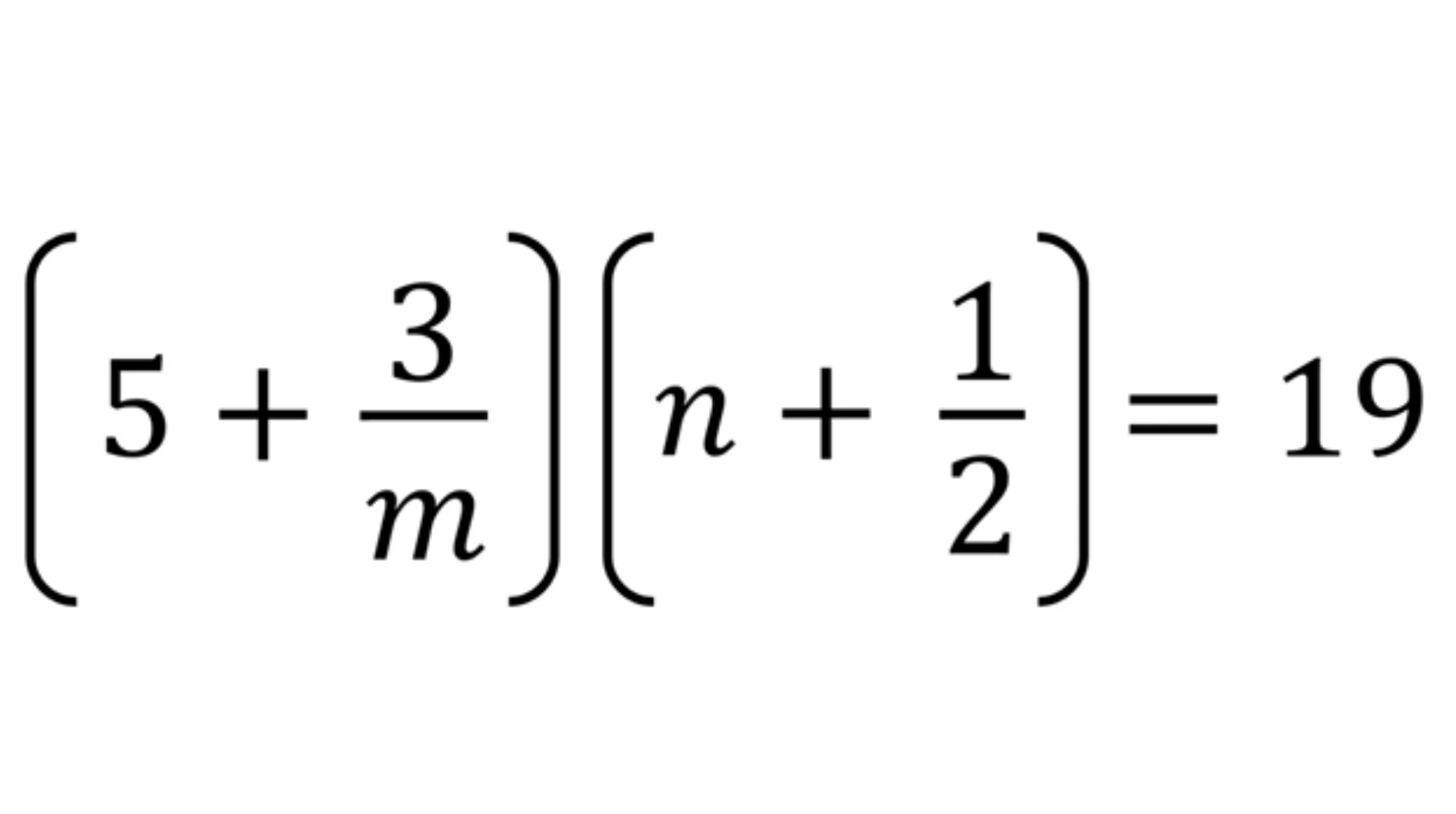
Полезно заметить, что Можно опустить округление в неравнестве, так как округление вверх стоит слева от знака меньше. Потом все упрощается до тождества. Немного спорный вопрос, а что происходит, если , но этот случай нам проблем не составит дальше и в итоге мы получим, что сумма 0 слагаемых равна 0. Целую часть можно вынести за знак суммы, получив и даже в случае все работает.
Эту сумму можно выразить, как. Далее, вспоминая, как мы боролись с граничными случаями, можно заметить, что первая сумма сокращается до:. В итоге получаем напомниаю, что. При этом, выше мы уже показали, что. Также, очевидно, что. Также, и взаимнопросты.
Поэтому, после одного рекуррентного перехода мы всегда останемся в том же общем случае, поэтому опять проверять граничные условия не надо. А база у рекурсии, если , то результат 0.
Еще можно остановится, если и выдать сумму арифметической прогресси. Или, если , то сумма ничего - ноль. Подобно алгоритму Эвклида для GCD, эта рекуррентная формула позволяет считать сумму за. Его еще можно итеративно реализовать и получить по памяти. Поиск Написать публикацию. Уровень сложности Сложный. Время на прочтение 6 мин. Примечание по оформлению Я буду активно пользоваться "аббревиатурами" в этой статье: всякое нудное объяснение я буду прятать в них.
Теги: литкод задачи алгоритмы математика. Хабы: Алгоритмы Математика. Комментарии Илья wataru.

Отправить сообщение. Комментарии Комментарии Лучшие за сутки Похожие. Серия занятий «Тренировки по алгоритмам 5. Время Место Онлайн.