Примеры вращательного движения,

Момент силы определяет скорость изменения углового положения тела и зависит от силы, приложенной к телу, и растояния от оси вращения до точки приложения силы. Посмотрите видео-объяснение темы Преподаватель Фоксфорда всё подробно расскажет и покажет. Читать ещёУгловое ускорение.
А ещё раздел с полезными материалами, календарь занятий и уведомления о предстоящих уроках. Твердое тело — тело, расстояние между любыми двумя точками которого сохраняется с течением времени. Различают два вида движения твердого тела: поступательное и вращательное. В ряде случаев тело совершает смешанное движение, т.
Поступательным называется такое движение твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе, т. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки.
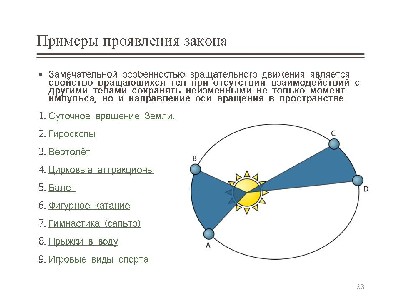
Вращательным называется такое движение твердого тела, при котором все его точки описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Меню Подобрать занятия. Учебник Избранные статьи. Скачайте мобильное приложение и читайте Фоксфорд Учебник на телефоне и планшете. Поступательное и вращательное движение твёрдого тела. На всех остальных поверхностях неподвижных в глобальной системе координат ничего задавать не нужно. Поверхности, которые неподвижны в глобальной системе координат, включая внешние границы региона должны быть поверхностями вращения, а «вращающиеся» поверхности могут быть любыми.
Вращение на подобласти ЛСК и Вращение задается в случае использования «скользящей поверхности» для той подобласти, в которой будет использована вращающаяся система координат. При этом, как и в случае задания вращения на регионе согласно п. Для подвижного тела может быть задан любой вид движения, в том числе и вращение.
FlowVision отображает скорость и другие векторные переменные в спутной системе координат. Это — глобальная абсолютная СК, совпадающая в данный момент времени с локальной относительной СК. Поэтому пользователь видит геометрическую модель расчетной области в локальной относительной СК, а векторные переменные — в абсолютной СК Рис. Однако для векторов существует также возможность отображения в относительной СК Рис.
Для этого необходимо задать параметры необходимой системы отсчёта в свойствах слоя «Векторы» в разделе Движущаяся СК. В зависимости от особенности и сложности моделируемого физического явления, происходящего в жидкости или газе, оно может быть смоделировано, как в абсолютной неподвижной рис. В данном случае подразумевается, что расчетная область или её часть подобласть вместе с частицами жидкости или газа рассматриваются в абсолютной неподвижной системе координат, в инерциальной системе отсчета рис.
Но при этом, в данном объеме могут существовать тела поверхности , которые испытывают вращение. В рамках данного подхода можно корректно описывать движение жидкости или газа около любого вращающегося твердого тела, моделируемого как модификатор «Подвижное тело». При этом задается закон вращения для «Подвижного тела» см. Таким же образом, без перехода в относительную систему координат, можно описать движение жидкости или газа около тела поверхности вращения, вращающегося вокруг своей оси вращения.
При этом, необходимо задать вращение на ГУ, соответствующем данной вращающейся поверхности см. Корректность подхода не теряется, при любом изначальном направлении потока жидкости или газа относительно данного тела.
В данном случае подразумевается, что расчетная область или её часть подобласть вместе с частицами жидкости или газа рассматриваются в относительной вращающейся системе координат, в неинерциальной системе отсчета рис.
В таком случае на частицы жидкости или газа действуют силы инерции см. Таким образом можно описать, движение жидкости или газа около тела, поверхности которого могут не являться поверхностью вращения, а само вращение происходит вокруг любой оси. При этом, чтобы учесть силы инерции, необходимо задавать для расчетной области регион или её части подобласти локальную вращающуюся систему координат для региона см.

Данный тип задач удобно решать в рамках похода, описанного в п. Задается ЛСК начало и направление осей в которой добавляется Вращение, для которого указывается Скорость, Центр и направление вращения см.
Задаётся вращения на поверхности.

Ограничение для моделирования теплопередачи: в случае задания ЛСК и Вращение на поверхности стенки или связанного граничного условия, необходимо учитывать, что локальный источник тепла не будет вращаться вместе с поверхностью и нагрев поверхности и области вблизи нее будет локальным, а не равномерным.
Задача - прямое движение автомобиля. Рассмотрим движение автомобиля в системе координат автомобиля, то есть в расчетной области автомобиль неподвижен — его движение моделируется скоростью набегающего потока, которая равна скорости автомобиля и с учетом ветра.
Во внешний объем «Автомобиль» вставляется как импортированный объект на котором задается модификатор "Подвижное тело". Для учета движения-вращения колес задается вращение на поверхностях колес с использованием ЛСК. В каждой ЛСК задается Вращение вектор угловой скорости.
Создаются отдельные граничные условия для каждой пары колес для которых в свойствах выбираются соответствующие ЛСК и Вращение рис. Примечание: для данной задачи движения автомобиля необходимо учитывать движение покрытия дороги относительно автомобиля, это можно сделать несколькими способами:.
Значение скорости задается компонентами вектора скорости в ЛСК и будет соответствовать скорости автомобиля с противоположным знаком. Задается вращение внешней области по отношению к вращающемуся телу. На граничном условии «вращающейся» поверхности также задаются ЛСК и Вращение геометрия «вращающейся» поверхности может быть любой см.
Моделирование ветровой турбины Вращение на регионе и ГУ поверхности лопаток. Задание вращения на граничном условии поверхности лопаток. Примечание: Лопатки могут вставляться как "подвижное тело" с отключенеим обновления так и быть частью основной геометрии Региона как подобласть. После вставки формируется вторая подобласть. В первой же подобласти которая будет расчетной добавляются поверхности лопаток. Тело будет физически вращаться, перестраивая каждый шаг расчетную сетку.
Вращающееся тело вставляется во внешнюю расчетную область как импортированный объект, на котором устанавливается Модификатор «Подвижное тело». Вращение с заданной угловой скоростью задается вектором угловой скорости компонент вектора X, Y и Z в глобальной СК см. Задание компонент вектора угловой скорости возможно формулой с помощью Редактора формул, зависящей от различных параметров, в том числе и расчетных. Вращение так же может быть задано под действием гидродинамических сил.
Для этого необходимо задать гидромоменты для соответствующих осей вращения, а также массово-инерционные характеристики, и, при необходимости, добавить ограничители для вращения — например, задать пространственную ось двумя точками в свойствах модификатора подвижного тела в ограничителях Степени свободы, тип — «2 степени свободы».
Ограничения: Задание движения подвижных тел весьма затратный метод в плане вычислительных ресурсов, поскольку подвижное тело изменяет свое положение на каждой итерации и происходит перестроение сетки вблизи подвижного тела — это существенно увеличивает время счета. Однако, подвижные тела становятся единственной возможностью моделирования в случае очень сложных законов движения или в составе сложных устройств.
Во внешний объем-Регион вставлены три импортированных объекта: основное тело вертолета и две лопасти. Для каждого импортированного объекта задан Модификатор-Подвижное тело. Отметим, что вторую лопасть можно создать как копию первой, где в свойствах подвижного тела изменить начальное положение — поворот вокруг оси Z на градусов. Для основного тела вертолета в свойствах подвижного тела отключено обновление - тело включено в расчет, но для него не задается движение.
Для лопастей вертолета задаем значения компонент вектора угловой скорости.
В данном случае Wz. При необходимости изменяем значение угловой скорости только в одном месте — пользовательская переменная - меняем значение пользовательской переменной.
Пользовательские величины могут быть и константами и переменными величинами, а также возможно задание вектора.

Вращение лопастей вокруг оси Z. Задание вращения для лопасти 1. Примечание: для минимизации количества расчетных ячеек при построении сетки вокруг вращающихся подвижных тел можно использовать следующий прием: помимо адаптации по поверхности можно задавать адаптацию в объеме цилиндра, окружающего лопасть см.
Для данных цилиндров следует задать Движение:Вращение синхронное с вращением лопастей. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым. Производная по времени от момента количества движения механической системы относительно неподвижной инерциальной системы отсчёта точки или центра инерции системы равна главному моменту относительно той же точки всех внешних сил, приложенных к системе.
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:. В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы.
Материал из Википедии — свободной энциклопедии. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии , проверенной 8 ноября года; проверки требуют 2 правки. У этого термина существуют и другие значения, см. Вращение значения.