Троичная система счисления, Системы счисления — ТолВИКИ

Однако для копирования и использования текста нужно зарегистрироваться в экосистеме Автор Задачу о наилучшей системе гирь рассматривал Лука Пачоли. Следовательно, в результате отбрасывания младших цифр числа получается наилучшее при данном количестве оставшихся цифр приближение этого числа, и округление не требуется.
В финал конкурса вышел еще один нижегородский школьник — Роман Лапин.
Макарычев сказал, что идея принадлежит не ему. Ее придумали в нашей стране задолго до него, но потом незаслуженно забыли. Казанским заводом математических машин было произведено 46 компьютеров Сетунь, 30 из них использовались в университетах СССР.
Тактовая частота процессора — кГц. DSSP похож на язык Forth, оба — примеры стековых языков программирования. Регистры регистр команд — 9 разрядов[3] регистр номера команды счетчик команд C — 5 разрядов[3] регистр переадресации УУ F — 5 разрядов[3] 2 9ти разрядных регистра, входной и выходной, в блоке управления вводом-выводом.
Вполне заслуженно - какую пользу она несёт? Двоичная проще как в реализации, так и в эксплуатации , так и надёжнее.
Из целочисленных систем счисления наибольшей плотностью записи информации обладает троичная, а не двоичная система исчисления. Троичная симметричная система счисления обладает тем свойством, что обеспечивает более простое представление отрицательных чисел в памяти компьютера. Троичный компьютер оперирует троичной логикой, первой и наиболее известной многозначной логикой.
В отличие от двоичной логики, где высказыванию присваивается значения либо «истинно», либо «ложно», троичная нечеткая логика имеет состояние «неизвестно». Преимущество трехзначной логики над бинарной легче всего продемонстрировать на примере операции сравнения двух чисел: здесь троичная логика сразу выдает результат больше, меньше или равно , а двоичной для ответа требуется сначала выяснить, больше ли первое второго, а затем убедиться, не больше ли второе первого.
Вполне заслуженно - это по крайней мере смешно.

А что я получу, сказав как можно использовать систему счисления с переменным основанием, в том числе с переменным основание не являющимся простым числом. Дак а что сделал ученик из Сарова-то?
Что значит «с блеском защитил идею»? В чём новизна его работы? Нам в университете рассказывали о том, что от троичной отказались, так как двоичная намного надёжней в плане помехоустойчивости и проще в реализации. А сейчас уже никто не будет переходить, так как все массовые компоненты - двоичные. IBM в своих публикациях также сообщает о троичной вычислительной технике, но активно не участвует в ней.
Ты странный. Я тебе одно - ты мне другое. Я тебе про массовое производство - ты об отдельных специализированных системах. А недостатки, которые я назвал, ты проигнорировал. Разницу между двоичными и троичными подходами в строении вычислительных машин можно проиллюстрировать на примере пешеходного перехода. Если рассматривать с точки зрения двоичного - ты можешь двигаться по переходу только в одну сторону. Если с точки зрения троичного подхода - ты можешь переходить как в одну сторону, так и в другую.
Не приходится, как в случае с двоичным, бежать до следующего перехода, если этот только в обратную сторону. К тому же при троичном представлении данных в ячейке памяти умещается больше значений - диапазон шире.
Это значит, что для того, чтобы представить число, этих ячеек понадобится меньше. Плюс у уравновешенного троичного кода его по-разному называют - уравновешенный, сбалансированный есть преимущество: каждый разряд содержит знак того значения, которое содержится в этом разряде. В данном случае у нас минус один, ноль и плюс один.
Для того чтобы выяснить, какой знак у всего числа, содержащегося в ячейке, достаточно взять первый ненулевой разряд и посмотреть, какой у него знак. В двоичной системе берёшь ячейку и смотришь: если там единица, то соответствующую степень двойки надо добавить к общей сумме. В случае с троичной системой если в ячейке плюс, то степень тройки необходимо добавить, а если минус, то вычесть. И соответственно там может лежать и отрицательное число, и положительное, и нулевое.
Здесь очень интересно проявляется особенность, которая есть во всех уравновешенных системах счисления - у них наилучшее округление. Не нужно никаких специальных алгоритмов для того, чтобы округлить число, достаточно просто отбросить ненужные знаки, и в оставшихся разрядах автоматически получится лучшее приближение числа. Уравновешенное троичное представление имеет интересную особенность: поскольку оно уравновешенное, то содержит как положительные, так и отрицательные значения.
То есть можно в некоторых алгоритмах добиться существенного прироста, например при сжатии. Здесь не нужно всегда только увеличивать словарь - в какой-то момент его можно и уменьшать.
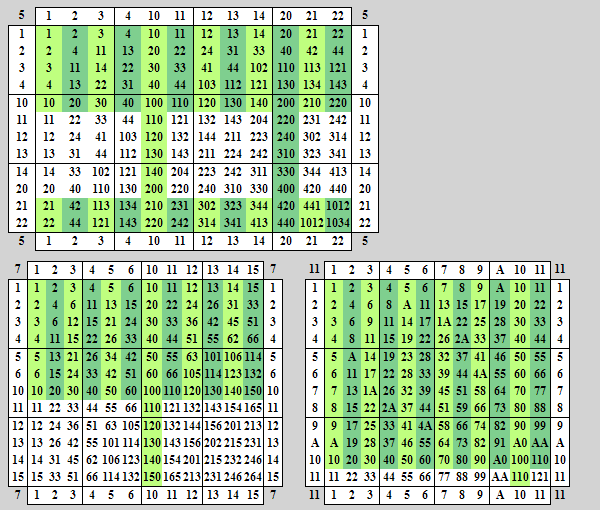
Ещё с древнего времени и по сей день рычажные весы оснащены подобием троичной системы. Знаменитый итальянский учёный Фибоначчи ещё в своё время предложил целочисленную симметричную троичную систему счисления. Как отметил известный французский учёный О.
Коши, таблица умножения в этой системе получилась короче примерно в четыре раза, если сравнивать с десятичной системой. Загрузи учебную работу и получи отформатированную версию всего через 30 секунд. Все сервисы Справочника в твоем телефоне! Просто напиши Боту, что ты ищешь и он быстро найдет нужную статью, лекцию или пособие для тебя! Включи камеру на своем телефоне и наведи на Qr-код.
Кампус Хаб бот откроется на устройстве.
Екатерина Андреевна Гапонько. Показать больше хлебных крошек Справочник Автор24 Статьи от экспертов Информатика Системы счисления Троичная система счисления числа Используй нейросеть AvtorGPT для своей учебы Создали собственный искусственный интеллект, чтобы помочь тебе с учебой в пару минут. Автор статьи. Статья написана экспертом Автор Определение 1.

Сервисы для учебы на 5 от руб. Готовые решения задач. AI-помощник для учебы.
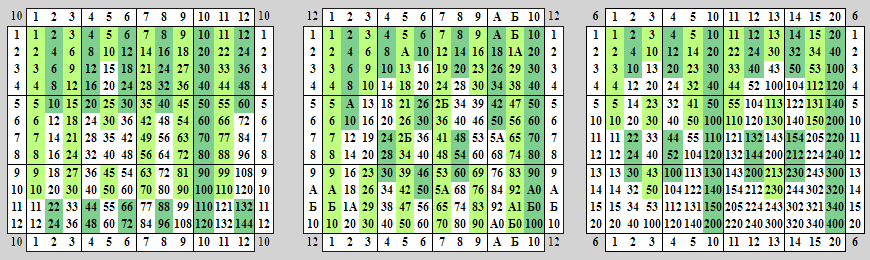
Определение 2. Помощь эксперта по теме работы. Замечание 1. Не понимаешь, как писать работу? Попробовать ИИ. Дата написания статьи: Наши статьи цитируют. Научные журналы. Google scholar. Похожие материалы по теме. Найди решение своей задачи среди 1 ответов.
Крупнейшая русскоязычная библиотека студенческих решенных задач. Найти решение задачи. Помощь со студенческой работой. Троичная система счисления основана на использовании трех символов: 0, 1 и 2. В отличие от двоичной системы, где используются только два символа 0 и 1 , троичная система позволяет представить числа более компактно и эффективно.
В троичной системе счисления каждая позиция символа имеет вес, который увеличивается вдвое с каждой последующей позицией. В результате получим число 10 в троичной системе. Троичная система счисления находит применение во многих областях, таких как электроника, информатика, криптография, математика и даже игры. Она позволяет более эффективно представлять и обрабатывать информацию, особенно в случаях, когда имеется большое количество различных состояний или вариантов.
Троичная система счисления является одной из множества возможных систем счисления и может быть использована вместо или в дополнение к десятичной и двоичной системам счисления в различных областях. В компьютерах и электронике, троичная система счисления имеет свои применения, хотя большинство систем счисления, используемых в этих областях, основаны на двоичной системе.
Одно из применений троичной системы счисления в компьютерах связано с решением проблемы потребления энергии. Переключение между двумя состояниями в двоичной системе требует большого количества энергии и приводит к выделению тепла. Однако, использование троичной системы позволяет сократить потребление энергии, так как переключение между тремя состояниями требует меньшего количества энергии и выделяет меньше тепла.
Также, троичная система счисления может быть использована для повышения плотности хранения информации на микросхемах. Вместо представления каждого бита информации двумя состояниями 0 и 1 в двоичной системе, троичная система позволяет использовать три состояния 0, 1 и 2 , что повышает плотность хранения информации и увеличивает емкость микросхемы. Троичная система счисления также используется в некоторых алгоритмах и математических операциях.
Например, в некоторых алгоритмах сжатия данных, троичные числа могут использоваться для представления определенных символов и комбинаций символов, что позволяет эффективнее сжимать и передавать данные.
В области электроники, троичные системы счетчиков могут использоваться для счета и управления временем. Например, троичные счетчики могут быть использованы в цифровых часах или таймерах, где третье состояние позволяет счетчику переключаться между часами, минутами и секундами.
Таким образом, троичная система счисления имеет свои применения в компьютерах и электронике, обеспечивая более эффективное использование энергии, повышение плотности хранения информации и расширение возможностей в алгоритмах и счетчиках.